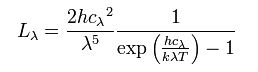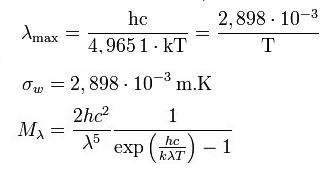Affichages
(Page créée avec « Les grandes lois du rayonnement en thermographie infrarouge = Loi de Planck = Présentation graphique de la loi de Planck La loi... ») |
|||
| (9 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | Les grandes lois du rayonnement en thermographie infrarouge | + | = Les grandes lois du rayonnement en thermographie infrarouge = |
| − | = Loi de Planck = | + | |
| + | Tiré majoritairement de: | ||
| + | * [http://fr.wikipedia.org/wiki/Loi_de_planck Loi de Planck] | ||
| + | * [http://fr.wikipedia.org/wiki/Loi_de_lambert loi de Lambert] | ||
| + | * [http://fr.wikipedia.org/wiki/Loi_du_d%C3%A9placement_de_Wien Loi du déplacement de Wien] | ||
| + | * [http://fr.wikipedia.org/wiki/Loi_de_stefan Loi de Stefan] | ||
| + | * [http://www.wiki-thermographie.net/index.php/Les_grandes_lois_du_rayonnement Loi de Bouguer] | ||
| + | |||
| + | == Loi de Planck == | ||
[[file:Loi_planck.png|thumb|right|300px|Présentation graphique de la loi de Planck]] | [[file:Loi_planck.png|thumb|right|300px|Présentation graphique de la loi de Planck]] | ||
La loi de Planck définit la distribution de luminance énergétique monochromatique du rayonnement thermique du corps noir en fonction de la température thermodynamique. | La loi de Planck définit la distribution de luminance énergétique monochromatique du rayonnement thermique du corps noir en fonction de la température thermodynamique. | ||
| Ligne 8 : | Ligne 16 : | ||
[[file:loi_planck.JPG]] | [[file:loi_planck.JPG]] | ||
| − | = Loi de Lambert = | + | == Loi de Fourier == |
| + | |||
| + | La conduction thermique est un transfert thermique spontané qui relie les zones de haute température vers celles de basse température. Elle est décrite par la loi dite ''de Fourier'' établie mathématiquement par Jean-Baptiste Biot en 1804 puis démontré de manière expérimentale par Fourier en 1822. | ||
| + | La loi de Fourier est une loi semi-empirique proche de la loi de Fick pour la diffusion de particule ou la loi d'Ohm pour la conduction électrique (Ohm s'est d'ailleurs inspiré d'un modèle thermique pour bâtir sa théorie). Ces trois lois peuvent s'interpréter de la même façon : la non-homogénéité d'un paramètre intensif provoque un transport spontané ayant une direction du plus intense vers le moins élevé visant à résorber le déséquilibre jusqu'à retour à l'équilibre du système. | ||
| + | On peut donc l'énoncer de la manière suivante:'':Dans des conditions stationnaires, le flux de transfert thermique par conduction est directement proportionnel à la conductivité thermique, à la section de passage, et à la différence de température entre les extrémités d'un parcours donné. Il est inversement proportionnel à la longueur du parcours.'' | ||
| + | |||
| + | [[file:loi_fourier.JPG]] | ||
| + | |||
| + | == Loi de Lambert == | ||
| + | |||
| + | La loi de Lambert indique que pour une source lumineuse orthotrope, l'émittance est proportionnelle à la luminance et le coefficient de proportionnalité est Pi. Autrement dit, si M désigne l'émittance et L la luminance, pour une source lumineuse orthotrope, on a : | ||
| + | |||
| + | [[file:loi_lambert.JPG]] | ||
| + | |||
| + | == Loi du déplacement de Wien == | ||
| + | |||
| + | La loi du déplacement de Wien, ainsi nommée d'après son découvreur Wilhelm Wien, est une loi physique selon laquelle une longueur d'onde à laquelle un corps noir émet le plus de flux lumineux énergétique est inversement proportionnelle à sa température. La loi de Wien est déduite de la loi de Planck du rayonnement du corps noir car celle-ci la corrige aussi. | ||
| − | La loi de | + | La loi de Wien décrit la relation liant la longueur d'onde λ<sub>max</sub>, correspondant au pic d'émission lumineuse du corps noir, et la température T (exprimée en kelvin). On retient généralement, en exprimant la longueur d'onde en mètre et la température en kelvin : |
| − | + | ||
| − | + | [[file:loi_wien.JPG]] | |
| − | + | == Loi de Stefan-Boltzmann == | |
| − | + | ||
| − | + | ||
| − | + | La loi de Stefan-Boltzmann ou de Stefan établit que la puissance totale rayonnée par unité de surface dans le demi-espace libre d'un corps noir s'exprime par la formule : | |
| − | + | M = σ.T<sup>4</sup> | |
| − | + | ||
| − | Où | + | Où σ est la constante de Stefan-Boltzmann (aussi appelée constante de Stefan). |
| − | = Loi de Bouguer = | + | == Loi de Bouguer == |
La loi de Bouguer décrit l'élément de flux quittant une source dS et parvenant au récepteur dR. Elle est à la base de l'étude des échanges radiatifs en thermique. d5φ(T) = L°λ(T). dS . dR. cosθ . cosθ'. dλ / D2 avec L°λ, luminance spectrique directionnelle émise par dS vers dR. <ref>[http://www.wiki-thermographie.net/index.php/Les_grandes_lois_du_rayonnement Les grandes lois du rayonnement], wiki-thermographie</ref> | La loi de Bouguer décrit l'élément de flux quittant une source dS et parvenant au récepteur dR. Elle est à la base de l'étude des échanges radiatifs en thermique. d5φ(T) = L°λ(T). dS . dR. cosθ . cosθ'. dλ / D2 avec L°λ, luminance spectrique directionnelle émise par dS vers dR. <ref>[http://www.wiki-thermographie.net/index.php/Les_grandes_lois_du_rayonnement Les grandes lois du rayonnement], wiki-thermographie</ref> | ||
| − | = Notes et références = | + | == Notes et références == |
<references/> | <references/> | ||
[[catégorie:article]] | [[catégorie:article]] | ||
Version actuelle en date du 21 décembre 2013 à 16:57
Sommaire |
[modifier] Les grandes lois du rayonnement en thermographie infrarouge
Tiré majoritairement de:
[modifier] Loi de Planck
La loi de Planck définit la distribution de luminance énergétique monochromatique du rayonnement thermique du corps noir en fonction de la température thermodynamique. La luminance énergétiquenote 1 monochromatique est un flux énergétique par unité de surface, par unité d'angle solide et par unité de longueur d'onde ; elle s'exprime donc en W·m-2·sr-1·m-1 en unités SI :
[modifier] Loi de Fourier
La conduction thermique est un transfert thermique spontané qui relie les zones de haute température vers celles de basse température. Elle est décrite par la loi dite de Fourier établie mathématiquement par Jean-Baptiste Biot en 1804 puis démontré de manière expérimentale par Fourier en 1822. La loi de Fourier est une loi semi-empirique proche de la loi de Fick pour la diffusion de particule ou la loi d'Ohm pour la conduction électrique (Ohm s'est d'ailleurs inspiré d'un modèle thermique pour bâtir sa théorie). Ces trois lois peuvent s'interpréter de la même façon : la non-homogénéité d'un paramètre intensif provoque un transport spontané ayant une direction du plus intense vers le moins élevé visant à résorber le déséquilibre jusqu'à retour à l'équilibre du système. On peut donc l'énoncer de la manière suivante::Dans des conditions stationnaires, le flux de transfert thermique par conduction est directement proportionnel à la conductivité thermique, à la section de passage, et à la différence de température entre les extrémités d'un parcours donné. Il est inversement proportionnel à la longueur du parcours.
[modifier] Loi de Lambert
La loi de Lambert indique que pour une source lumineuse orthotrope, l'émittance est proportionnelle à la luminance et le coefficient de proportionnalité est Pi. Autrement dit, si M désigne l'émittance et L la luminance, pour une source lumineuse orthotrope, on a :
[modifier] Loi du déplacement de Wien
La loi du déplacement de Wien, ainsi nommée d'après son découvreur Wilhelm Wien, est une loi physique selon laquelle une longueur d'onde à laquelle un corps noir émet le plus de flux lumineux énergétique est inversement proportionnelle à sa température. La loi de Wien est déduite de la loi de Planck du rayonnement du corps noir car celle-ci la corrige aussi.
La loi de Wien décrit la relation liant la longueur d'onde λmax, correspondant au pic d'émission lumineuse du corps noir, et la température T (exprimée en kelvin). On retient généralement, en exprimant la longueur d'onde en mètre et la température en kelvin :
[modifier] Loi de Stefan-Boltzmann
La loi de Stefan-Boltzmann ou de Stefan établit que la puissance totale rayonnée par unité de surface dans le demi-espace libre d'un corps noir s'exprime par la formule :
M = σ.T4
Où σ est la constante de Stefan-Boltzmann (aussi appelée constante de Stefan).
[modifier] Loi de Bouguer
La loi de Bouguer décrit l'élément de flux quittant une source dS et parvenant au récepteur dR. Elle est à la base de l'étude des échanges radiatifs en thermique. d5φ(T) = L°λ(T). dS . dR. cosθ . cosθ'. dλ / D2 avec L°λ, luminance spectrique directionnelle émise par dS vers dR. [1]
[modifier] Notes et références
- ↑ Les grandes lois du rayonnement, wiki-thermographie