Émissivité et thermographie: la zone interdite : Différence entre versions

Version du 14 août 2013 à 11:05

Émissivité et thermographie: la zone interdite

La thermographie semble simple de prime abord, on vise une scène, on met au net (souvent en manuel ce qui est déjà une surprise pour beaucoup), un petit serrage de la plage des températures (appelé le gain) et enfin, on presse la gâchette et on obtient son image.

Dans la pratique, si l'on désire avoir une idée des températures, cela devient vite un peu plus compliqué, chaque corps a en fait son émissivité propre liée à la nature de sa surface, son état, sa structure, ...^[1]

Un corps parfaitement réfléchissant a une émissivité de 0 et un corps parfait absorbant (corps noir) à une émissivité de 1.

La majorité du temps, il vaut mieux travailler avec une émissivité de 1 (en mode absolu) et recalibrer à froid, devant l'ordinateur.

Cependant, la température réelle est relativement facile à calculer pour les objets dont l'émissivité est entre 1 et 0,7 (papier blanc ou les métaux totalement oxydés pour le 0.7).

En-dessous de 0.7 et jusque 0.5, le matériel et le savoir-faire de l'opérateur devient beaucoup plus essentiel.

En-dessous de 0.5, il devient vraiment illusoire d'avoir une vraie valeur de température et la dextérité nécessaire demande un environnement contrôlé et une bonne dose d'expertise, on sera de toute manière la plupart du temps dans des valeurs approchées.

Exemple pratique

Voici un petit brûle-parfum alimenté par une bougie chauffe-plat, pas trop méchant au niveau température et restant relativement dans la gamme de température observable par la caméra disponible, une FLIR E30BX.

L'avantage d'utiliser des pièces de monnaies c'est que ce sont des objets résistants, calibrés et à la composition physico-chimique rigoureuse. Cependant, ils restent oxydables et là se situe l'intérêt, la pièce de gauche est oxydée irrégulièrement tandis que celle de droit a été simonisée pour lui rendre une pureté maximale.

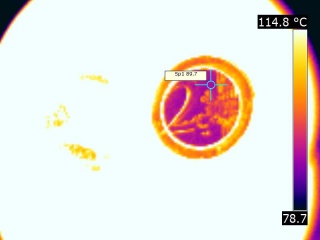
Résultat en image de la thermographie:

Nous constatons donc bien que deux pièces strictement identiques n'ont pas la même émissivité thermique une fois soumises à une source de chaleur commune. Les pièces sont en métal qui sont un excellent conducteur de chaleur et placées directement par-dessus la source thermique, leur température devrait donc approcher celle du fond du creuset.

Approchons la température réelle

Néanmoins, il est possible d'approcher la température d'une pièce à faible émissivité en la couvrant d'un matériau adhérant à forte émissivité.

Voici le résultat en image:

Le défaut, c'est qu'il n'est pas possible de connaître l'émissivité exacte d'un collant, il reste de la colle dessus, on le fait souffrir en le détachant, c'est relativement chaud donc souffrant de dégradations, ... En tous les cas, une prise de température avec un thermocouple montre une température de l'ordre de 89°C tandis que l'observation de la caméra nous amène vers 86-87°C.

Après quelques calculs, cela représente une émissivité de l'ordre de 0.11. Or les pièces de monnaies de deux euros sont composée d'un alliage: laiton de nickel pour la pièce intérieure et cupro-nickel pour l'anneau extérieur.Les émissivités de cupro-nickel se situent entre 0,05 et 0,15 et celles du laiton de nickel entre 0 et 0,3 ^[2] Nous tombons donc bien dans les plages observées mais avec des marges d'erreurs énormes. 2°C d'écart entre la vision thermique et le thermocouple, des incertitudes d'au moins 10% dans l'émissivité.

Pour déterminer la vérité, il faudrait déjà un bon labo, pour deux simples pièces de monnaies. Remarquons aussi que la pièce corrodée, sur ses parties très oxydées s'approche énormément des mesures de températures vraies

Le métal, ce casse-tête instable

Le métal est souvent "brillant" sauf que brillant en thermographie n'est pas toujours non plus synonyme de basse émissivité.

Un nickel est parfois si brillant quand il est poli qu'il peut devenir réflecteur thermique quasi-absolu, un miroir n'est jamais que du verre avec une couche de métal brillant en-dessous, son émissivité est haute: 0.97 mais c'est son comportement spéculaire qui pose problème (on voit plus l'environnement que la température du verre).

Le métal non oxydé fait souvent les deux, non seulement il est souvent très spéculaire mais en plus son émissivité est très basse. Tandis qu'une fois oxydé, il peut atteindre des valeurs de 0.6 voire 0.8 mais comment déterminer son degré d'oxydation et, pire encore, les possibles amalgames entre son oxydation et divers autres éléments de l'environnement.

Corrigeons l'émissivité alors?

C'est une possibilité mais voici le résultat, complètement inversé:

Donc le résultat n'est pas tellement plus exploitable, de plus la marge d'erreur devient énorme.

La zone interdite

Voici donc la fameuse zone interdite, en-deçà de 0.5 d’émissivité, si possible se cantonner à la plage 0.7-1.

Voici maintenant notre pièce brillante toute seule mais toujours chauffée:

Plaçons le thermocouple sur le centre: de l'ordre de 124°C donc désormais une émissivité de 0.08 contre 0.11 précédemment. Entre la marge d'erreur du thermocouple et celle de la caméra, l'observation est trop délicate, les deux valeurs sont crédibles mais la marge d'erreur trop importante. D'autant que le plafond réel de cette caméra est 120°C même si s'affiche jusque 150°C. Or plus vous atteignez les limites d'un instrument de mesure ou d'observation, moins il est précis.

Conclusions

Le métal n'est pas spécialement l'ami des caméras thermiques, l'oxydation aide mais la quantifier est difficile. Donc recouvrir le métal d'une couche opaque non réfléchissante et à basse émissivité une bonne idée sinon, une pièce qui paraît une trentaine de degrés à la caméra en fait en réalité autour de 100°C donc risque de brûlures, accidents, surcharges, ... La thermographie, dans ces cas-là est plutôt réservée aux laboratoires avec des caméras très précises et sensibles mais aussi des échantillons et des conditions d'observation maîtrisées ainsi que des opérateurs très expérimentés.

Voir aussi

Cube de Leslie, premier dispositif destiné à mettre en évidence et à mesurer les différences d'émissivité des surface.

Sources

1. ↑ Infrared Training Center, édition 2010 du manuel du niveau certifiant I
2. ↑ Table d'émissivité des métaux