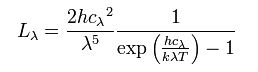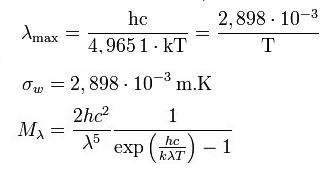Affichages
(→Les grandes lois du rayonnement en thermographie infrarouge) |
|||
| Ligne 9 : | Ligne 9 : | ||
* [http://www.wiki-thermographie.net/index.php/Les_grandes_lois_du_rayonnement Loi de Bouguer] | * [http://www.wiki-thermographie.net/index.php/Les_grandes_lois_du_rayonnement Loi de Bouguer] | ||
| − | = Loi de Planck = | + | == Loi de Planck == |
[[file:Loi_planck.png|thumb|right|300px|Présentation graphique de la loi de Planck]] | [[file:Loi_planck.png|thumb|right|300px|Présentation graphique de la loi de Planck]] | ||
La loi de Planck définit la distribution de luminance énergétique monochromatique du rayonnement thermique du corps noir en fonction de la température thermodynamique. | La loi de Planck définit la distribution de luminance énergétique monochromatique du rayonnement thermique du corps noir en fonction de la température thermodynamique. | ||
| Ligne 18 : | Ligne 18 : | ||
== Loi de Lambert == | == Loi de Lambert == | ||
| − | La loi de Lambert indique que pour une source lumineuse orthotrope, l'émittance est proportionnelle à la luminance et le coefficient de proportionnalité est | + | La loi de Lambert indique que pour une source lumineuse orthotrope, l'émittance est proportionnelle à la luminance et le coefficient de proportionnalité est Pi. Autrement dit, si M désigne l'émittance et L la luminance, pour une source lumineuse orthotrope, on a : |
[[file:loi_lambert.JPG]] | [[file:loi_lambert.JPG]] | ||
| Ligne 24 : | Ligne 24 : | ||
== Loi du déplacement de Wien == | == Loi du déplacement de Wien == | ||
| − | La loi du déplacement de Wien, ainsi nommée d'après son découvreur Wilhelm Wien, est une loi physique selon laquelle une longueur d'onde à laquelle un corps noir émet le plus de flux lumineux énergétique est inversement proportionnelle à sa température. La loi de Wien est déduite de la loi de Planck du rayonnement du corps noir car | + | La loi du déplacement de Wien, ainsi nommée d'après son découvreur Wilhelm Wien, est une loi physique selon laquelle une longueur d'onde à laquelle un corps noir émet le plus de flux lumineux énergétique est inversement proportionnelle à sa température. La loi de Wien est déduite de la loi de Planck du rayonnement du corps noir car celle-ci la corrige aussi. |
La loi de Wien décrit la relation liant la longueur d'onde λ<sub>max</sub>, correspondant au pic d'émission lumineuse du corps noir, et la température T (exprimée en kelvin). On retient généralement, en exprimant la longueur d'onde en mètre et la température en kelvin : | La loi de Wien décrit la relation liant la longueur d'onde λ<sub>max</sub>, correspondant au pic d'émission lumineuse du corps noir, et la température T (exprimée en kelvin). On retient généralement, en exprimant la longueur d'onde en mètre et la température en kelvin : | ||
Version du 20 décembre 2013 à 14:33
Sommaire |
Les grandes lois du rayonnement en thermographie infrarouge
Tiré majoritairement de:
Loi de Planck
La loi de Planck définit la distribution de luminance énergétique monochromatique du rayonnement thermique du corps noir en fonction de la température thermodynamique. La luminance énergétiquenote 1 monochromatique est un flux énergétique par unité de surface, par unité d'angle solide et par unité de longueur d'onde ; elle s'exprime donc en W·m-2·sr-1·m-1 en unités SI :
Loi de Lambert
La loi de Lambert indique que pour une source lumineuse orthotrope, l'émittance est proportionnelle à la luminance et le coefficient de proportionnalité est Pi. Autrement dit, si M désigne l'émittance et L la luminance, pour une source lumineuse orthotrope, on a :
Loi du déplacement de Wien
La loi du déplacement de Wien, ainsi nommée d'après son découvreur Wilhelm Wien, est une loi physique selon laquelle une longueur d'onde à laquelle un corps noir émet le plus de flux lumineux énergétique est inversement proportionnelle à sa température. La loi de Wien est déduite de la loi de Planck du rayonnement du corps noir car celle-ci la corrige aussi.
La loi de Wien décrit la relation liant la longueur d'onde λmax, correspondant au pic d'émission lumineuse du corps noir, et la température T (exprimée en kelvin). On retient généralement, en exprimant la longueur d'onde en mètre et la température en kelvin :
Loi de Stefan-Boltzmann
La loi de Stefan-Boltzmann ou de Stefan établit que la puissance totale rayonnée par unité de surface dans le demi-espace libre d'un corps noir s'exprime par la formule :
M = σ.T4
Où σ est la constante de Stefan-Boltzmann (aussi appelée constante de Stefan).
Loi de Bouguer
La loi de Bouguer décrit l'élément de flux quittant une source dS et parvenant au récepteur dR. Elle est à la base de l'étude des échanges radiatifs en thermique. d5φ(T) = L°λ(T). dS . dR. cosθ . cosθ'. dλ / D2 avec L°λ, luminance spectrique directionnelle émise par dS vers dR. [1]
Notes et références
- ↑ Les grandes lois du rayonnement, wiki-thermographie